(01)王道数据结构-时间复杂度

算法1： 逐步递增型爱你

#include<stdio.h>
void loveYou(int n);
int main(void) {
    loveYou(3000);
    return 0;
}

void loveYou(int n) {  //n为问题规模   
    int i = 1;         //爱你的程度
    while (i <= n) {   //每次+1
        i++;
        printf("I Love You %d\n", i);
    }
    printf("I Love You More Than %d\n", n);
}

(一)代码分析：

(1)语句频度

第09行：执行了1次

第10行：执行了3001次

第11行：执行了3000次

第12行：执行了3000次

第14行：执行了1次

T(3000) = 1 + 3001 + 2*3000 + 1

(2)时间复杂度

时间开销与问题规模n之间的关系

T(n) = 3n + 3

实际上时间复杂度只考虑阶数高的部分，高阶的常数项可以忽略

故本代码时间复杂度为: T(n) = n

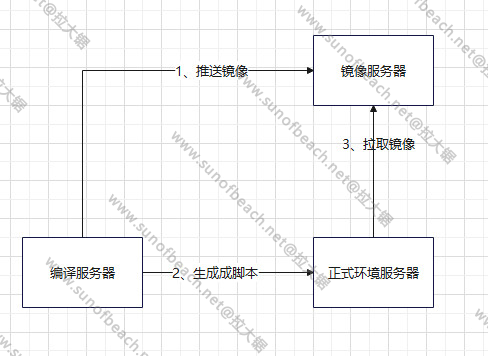
(二)运算规则

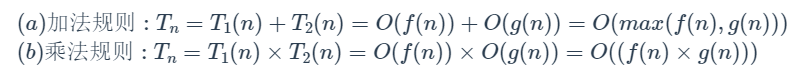
(三)时间复杂度排序

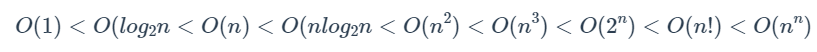
记忆口诀：常对幂指阶

算法2： 嵌套循环型爱你

#include<stdio.h>
void loveYou(int n);
int main(void) {
    loveYou(5);
    return 0;
}

void loveYou(int n) {  //n为问题规模   
    int i = 1;         //爱你的程度
    while (i <= n) {   //每次+1
        i++;
        printf("I Love You %d\n", i);
        for (int j = 1; j <= n; j++) { //嵌套循环两层
            printf("I am Iron Man\n");//内层循环共执行n*n次
        }
    }
    printf("I Love You More Than %d\n", n);
}

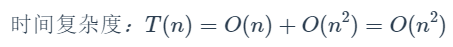
结论：

(1)顺序执行的代码只会影响常数项，可以忽略

(2)只需要挑循环中的一个基本操作分析它的执行次数与n的关系即可

(3)如果有多层循环嵌套，只需关注最深层循环循环了几次

算法3： 指数递增型爱你

#include<stdio.h>
void loveYou(int n);
int main(void) {
    loveYou(100);
    return 0;
}

void loveYou(int n) {  //n为问题规模   
    int i = 1;         //爱你的程度
    while (i <= n) {   
        i = i * 2;          //每次翻倍
        printf("I Love You %d\n", i);
    }
    printf("I Love You More Than %d\n", n);
}

时间复杂度分析：

(1)最深层语句频度为x

(2)循环结束时满足:

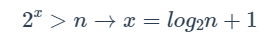
(3)时间复杂度:

算法4： 搜索数字型爱你

#include<stdio.h>
void loveYou(int flag[], int n);
int main(void) {
    int flag[] = {1,2,3,4,5,6,7,8,9};
    loveYou(flag,5);
    return 0;
}

void loveYou(int flag[], int n) {  //n为问题规模   
    printf("I Am Iron Man\n");
    for (int i = 0; i < n; i++) {
        if (flag[i] == n) {
            printf("I Love You %d\n", i);
            break;
        }
    }
}

时间复杂度分析：

最好情况： 元素n在第一个位置，时间复杂度为T(n)=O(1)

最坏情况： 元素n在最后一个位置，时间复杂度为T(n)=O(n)

平均情况： 元素n在任意一个位置的概率为1/n，时间复杂度为T(n)=O(n)

引申出最好时间复杂度，最坏时间复杂度，平均时间复杂度